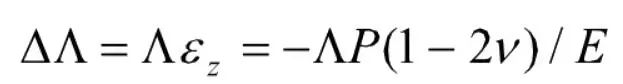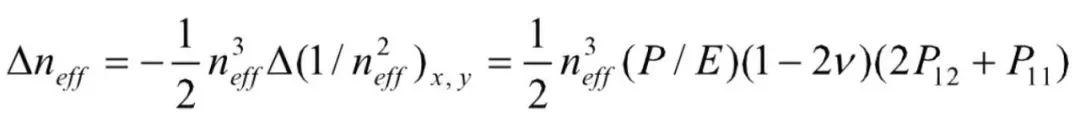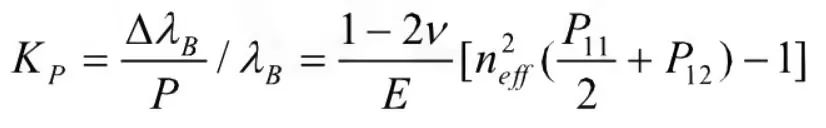光纤布拉格光栅(FBG)传感器的传感原理
布拉格光栅(FBG)是折射率呈周期性分布的光纤,其特点是反射某一波长的光,称为其中心波长。当FBG自身物理折射率周期在外界变量的影响下改变时,其中心波长也随之改变,且呈线性关系。利用中心波长的变量与外界力(温度等)的变量相对应的关系,可以实现应变、温度、位移、加速度等参量的测试。
.png)
.png) 光纤光栅的Bragg波长是随光栅的周期和纤芯模的有效折射率变化的,因此Bragg波长对于外界力、热负荷等极为敏感。
光纤光栅的Bragg波长是随光栅的周期和纤芯模的有效折射率变化的,因此Bragg波长对于外界力、热负荷等极为敏感。
应变和压力影响Bragg波长是由于光栅周期的伸缩以及弹光效应引起的,而温度影响Bragg波长是由于热膨胀效应和热光效应引起的。当外界的温度、应力和压力等参量发生变化时,Bragg波长的变化可表示为: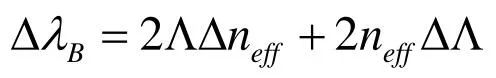 1温度传感原理
1温度传感原理
温度影响 Bragg波长是由热膨胀效应和热光效应引起的。假设均匀压力场和轴向应力场保持恒定,由热膨胀效应引起的光栅周期变化为:
式中α为光纤的热膨胀系数。热光效应引起的折射率变化为: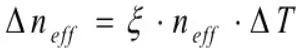 这里,ξ为光纤的热光系数,表示折射率随温度的变化率。可知Bragg光栅的波长在变化的温度场中表达式为:
这里,ξ为光纤的热光系数,表示折射率随温度的变化率。可知Bragg光栅的波长在变化的温度场中表达式为:
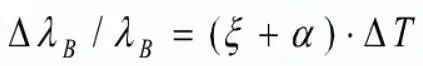 Bragg波长的变化与温度之间的变化有良好的线性关系,光栅的温度灵敏度为:
Bragg波长的变化与温度之间的变化有良好的线性关系,光栅的温度灵敏度为:
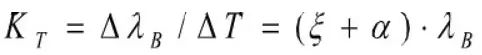 2应变传感原理
2应变传感原理
应变影响Bragg波长是由于光栅周期的伸缩和弹光效应引起的。
假设光纤光栅仅受轴向应力作用,温度场和均匀压力场保持恒定。轴向应力会引起光栅栅距的改变 :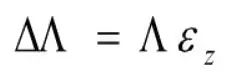 有效折射率的变化为:
有效折射率的变化为:
 式中,Pij是弹光系数,v是纤芯材料泊松比(下同)。
式中,Pij是弹光系数,v是纤芯材料泊松比(下同)。
沿z轴方向传播的光波所经受的折射率的变化为: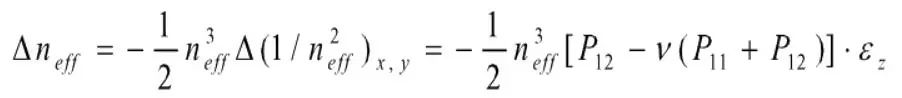 定义有效弹光系数:
定义有效弹光系数:
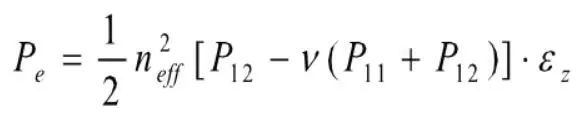 综合可得应变的灵敏度:
综合可得应变的灵敏度:
 若沿光纤轴向施加拉力F,根据胡克定律,光纤产生的轴向应变为:
若沿光纤轴向施加拉力F,根据胡克定律,光纤产生的轴向应变为:
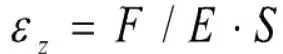 式中E为光纤的杨氏模量,S为光纤面积,该拉力引起的Bragg波长变化:
式中E为光纤的杨氏模量,S为光纤面积,该拉力引起的Bragg波长变化:
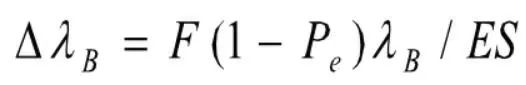 3压力灵敏度
3压力灵敏度
压力影响也是由光栅周期的伸缩和弹光效应引起的,假设温度场和轴向拉力保持恒定,光纤处于一个均匀压力场P中,轴向应变会使光栅的栅距改变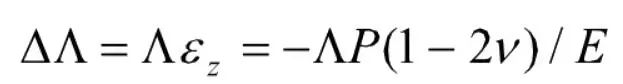 有效折射率的变化为:
有效折射率的变化为:
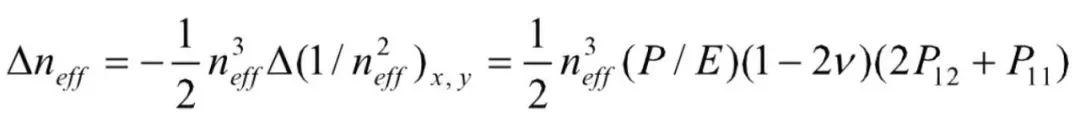 光纤光栅的压力灵敏度为:
光纤光栅的压力灵敏度为:
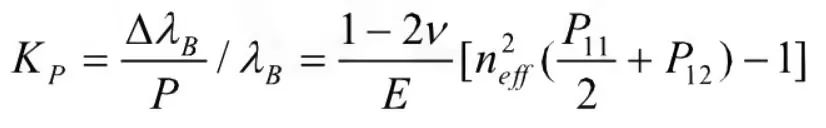 由于掺杂成分和掺杂浓度的不同,各种光纤光栅的压力灵敏度差别较大。
由于掺杂成分和掺杂浓度的不同,各种光纤光栅的压力灵敏度差别较大。
.png)
.png)
应变和压力影响Bragg波长是由于光栅周期的伸缩以及弹光效应引起的,而温度影响Bragg波长是由于热膨胀效应和热光效应引起的。当外界的温度、应力和压力等参量发生变化时,Bragg波长的变化可表示为:
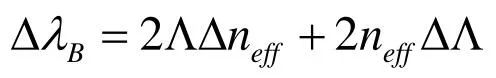
温度影响 Bragg波长是由热膨胀效应和热光效应引起的。假设均匀压力场和轴向应力场保持恒定,由热膨胀效应引起的光栅周期变化为:

式中α为光纤的热膨胀系数。热光效应引起的折射率变化为:
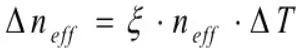
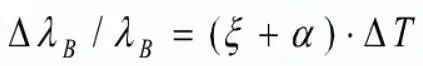
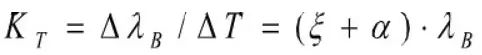
应变影响Bragg波长是由于光栅周期的伸缩和弹光效应引起的。
假设光纤光栅仅受轴向应力作用,温度场和均匀压力场保持恒定。轴向应力会引起光栅栅距的改变 :
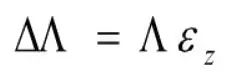

沿z轴方向传播的光波所经受的折射率的变化为:
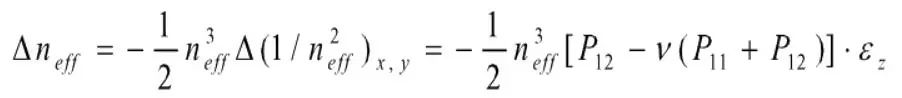
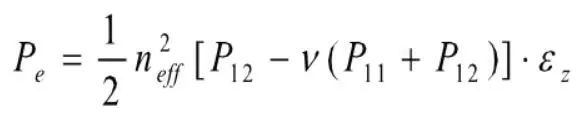

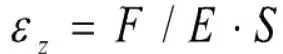
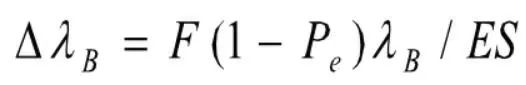
压力影响也是由光栅周期的伸缩和弹光效应引起的,假设温度场和轴向拉力保持恒定,光纤处于一个均匀压力场P中,轴向应变会使光栅的栅距改变